142. Linked List Cycle II

142. Linked List Cycle II Medium

Given a linked list, return the node where the cycle begins. If there is no cycle, return null.

There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail’s next pointer is connected to. Note that pos is not passed as a parameter.

Notice that you should not modify the linked list.

Follow up:

Can you solve it using O(1) (i.e. constant) memory?

Example 1:

1
2
3

Input: head = [3,2,0,-4], pos = 1
Output: tail connects to node index 1
Explanation: There is a cycle in the linked list, where tail connects to the second node.

Example 2:

1
2
3

Input: head = [1,2], pos = 0
Output: tail connects to node index 0
Explanation: There is a cycle in the linked list, where tail connects to the first node.

Example 3:

1
2
3

Input: head = [1], pos = -1
Output: no cycle
Explanation: There is no cycle in the linked list.

Constraints:

• The number of the nodes in the list is in the range [0, 104].
• -105 <= Node.val <= 105
• pos is -1 or a valid index in the linked-list.

思路：

思路一：

大体思路还是和 141 一样的，唯一的后续操作就是：让相遇点和开始点一起再向后走，这两个点再次相遇的点就是入口点，具体可以参考下面的图和数学证明：

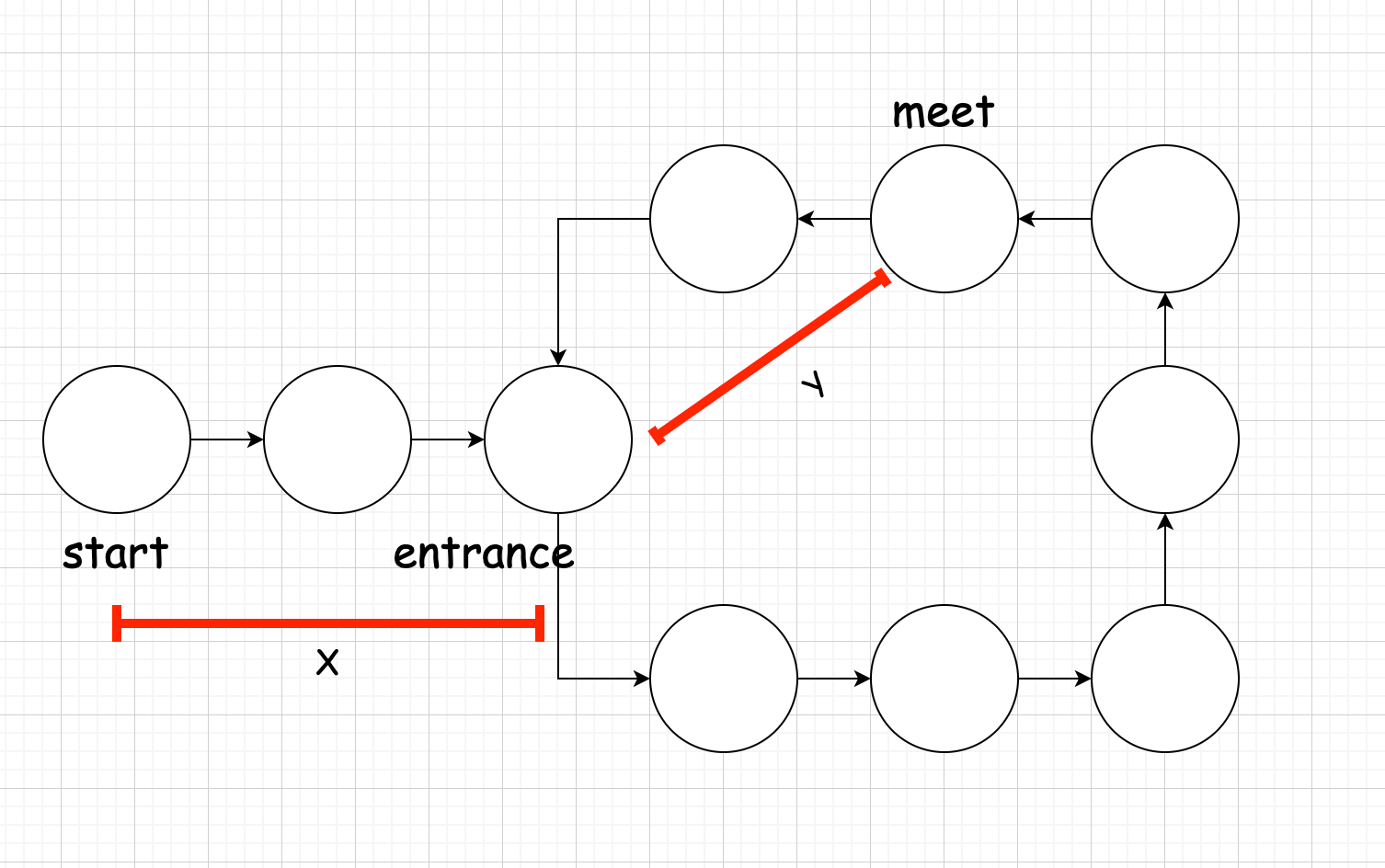
数学证明

条件：环的结点数 N、开始点到入口点距离 X、入口点到相遇点距离 Y (逆时针的距离，上图中长的那部分)

假设：slow 结点总共走了 T 步到相遇点；则 fast 结点共走了 2T 步

​ slow 结点总共走了 K1 圈； fast 结点共走了 K2 圈

则：

T = X + K1 * N + Y :one:

2T = X + K2 * N + Y :two:

化简：

T = (K2 - K1) * N

带到 :one: 中：

X = (K2 - 2K1 -1) * N + (N - Y)

其中：

(N - Y) 表示相遇点到入口点的距离

这时候就可以说：我相遇点的结点向前走了 (K2 - 2K1 -1) 圈回到了相遇点，再走了 (N - Y) 到了入口点

简直就是 Amazing 啊！

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

public ListNode detectCycle(ListNode head) {
    ListNode slow = head, fast = head;
    ListNode temp = null;
    while (fast != null && fast.next != null) {
        slow = slow.next;
        fast = fast.next.next;
        if (slow == fast) {
            temp = slow;
            while (head != temp) {
                head = head.next;
                temp = temp.next;
            }
            return head;
        }
    }
    return null;
}

时间复杂度：O()

空间复杂度：O()