Queue

重学算法系列

发布于：2020年11月24日

次浏览

一、OverView

在前面已经看过受限的线性序列：栈

在本章中可以看一下另外一个受限的线性序列：队列

在本章中可以看到：

🐢 : 首先对比一下栈，并介绍一下队列的特性

🐷 : 在这一小节中分别用数组和链表实现一下队列，主要是用数组实现

🐭 : 在这一小节主要介绍一下几个特殊的队列，其中主要是优先队列和双端队列

🐂 : 由于在 Java 中，队列是一个接口，简单看一下实现类

二、特性

首先来回忆一下栈的特性：先进后出，后进先出

而队列的特性就是：先进先出，后进后出

可以看一下下面的例子：

字符串 “wang” 依次入队，随后再出队（省略部分步骤）

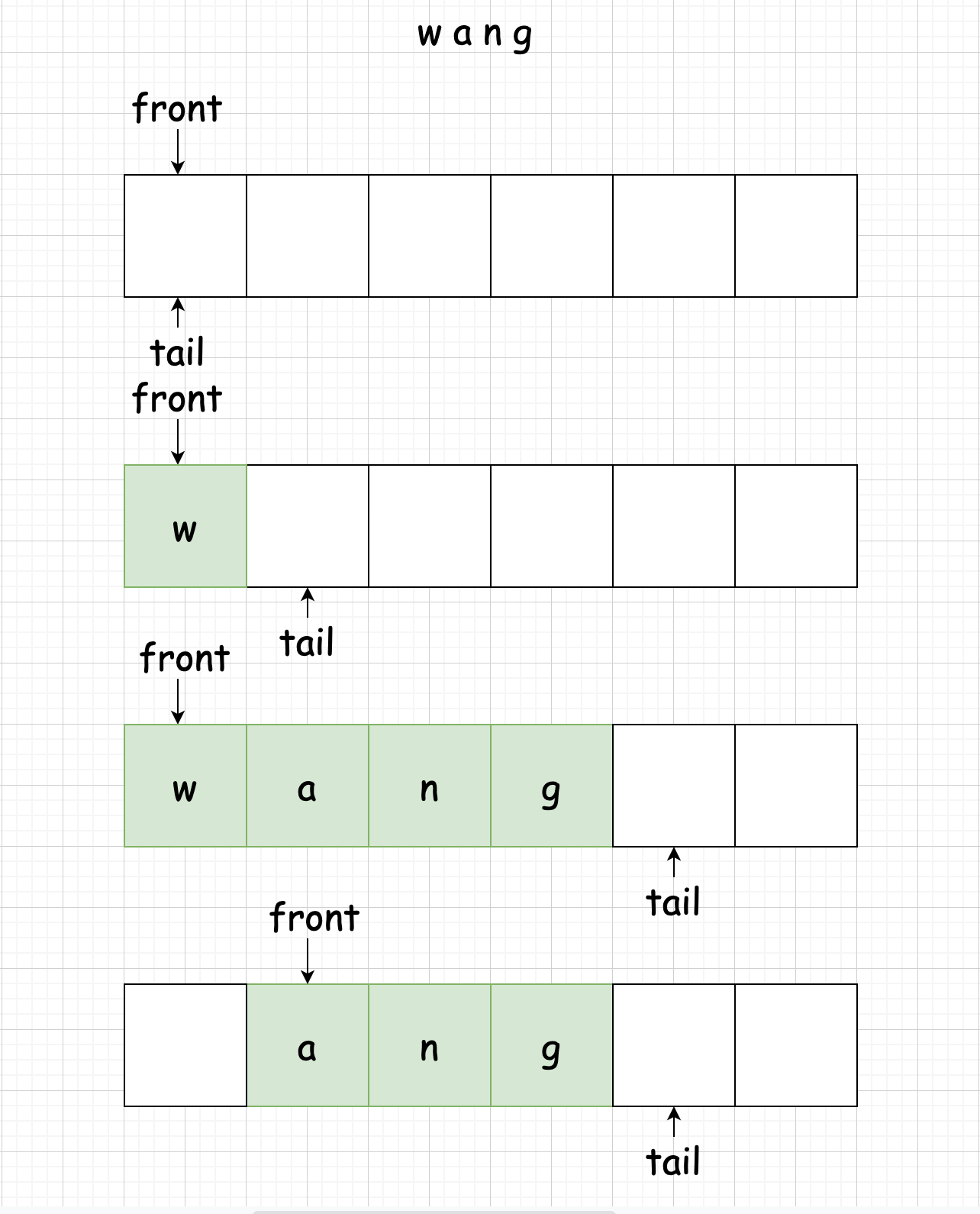
三、实现队列

3.1 数组实现

首先我们要知道有哪些操作：

只在队尾进行入队的操作：enqueue
只在队头进行出队的操作：dequeue

public class LC0000ArrayQueue {

    private String[] elements;

    private int capacity = 0;

    private int front = 0;

    private int tail = 0;

    public LC0000ArrayQueue(int n) {
        elements = new String[n];
        capacity = n;
    }

    // enqueue
    public boolean enqueue(String element) {
        if (tail == capacity) return false;
        elements[tail] = element;
        tail++;
        return true;
    }

    // dequeue
    public String dequeue() {
        if (front == tail) return null;
        String res = elements[front];
        front++;
        return res;
    }

}

但是仔细想想这个是有问题的，就拿上面那个例子来说，它全部入队和全部出队后的结果应该是这样：

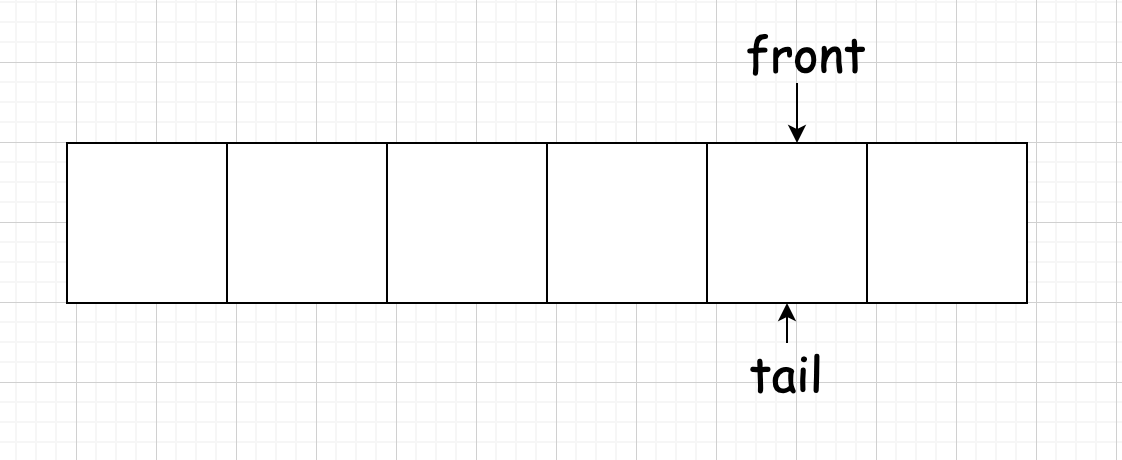
那么左边的空间就没有再使用了，如何解决这个问题呢？来考虑一下在数组中是如何解决这个问题，数组中删除一个元素，然后移动把这个元素后的所有数据都向前移动一位。

那么在这里只需要出队一个元素，随后把所有元素向前移动一位即可。但是这个每出队一个元素就移动一位，时间复杂度为 O(n)，稍微优化一下，只在我们需要它的时候才进行移动操作。那么我们什么时候是需要到这些空余的空间呢，是不是只有在元素入队的时候才需要，所以只需要在入队的时候进行数据搬移的操作即可，代码如下：

// enqueue
public boolean enqueue(String element) {
    if (tail == capacity) {
        // queue is full
        if (front == 0) return false;
        for (int i = front; i < elements.length; i++) {
            elements[i - front] = elements[i];
        }
        tail -= front;
        front = 0;
    }
    elements[tail] = element;
    tail++;
    return true;
}

首先要判断一下队列是不是真的满了
如果不是满的，就可以将 front 到 tail 的元素全部搬到 0 到 tail - front 的位置

3.2 链表实现

用链表实现的话，就不用考虑 capacity 的问题了，理论上在内存足够的情况下，可以无限入队，

public class LC0000LinkedListQueue {

    private Node front;

    private Node tail;

    // enqueue
    public void enqueue(String element) {
        if (tail == null) {
            Node next = new Node(element, null);
            front = next;
            tail = next;
        }
        else {
            tail.next = new Node(element, null);
            tail = tail.next;
        }
    }

    // dequeue
    public String dequeue() {
        if (front == tail) return null;
        String res = front.val;
        front = front.next;
        if (front == null) {
            tail = null;
        }
        return res;
    }

}


class Node {

    public String val;

    public Node next;

    public Node(String val) {
        this.val = val;
    }

    Node(String val, Node next) {
        this.val = val;
        this.next = next;
    }
}

四、一些特殊的队列

4.1 循环队列

在上面用数组实现队列时，由于队列的特性使得我们已经将其进行了一次优化，在每次进行入队操作时都要有条件的进行一次数据移动操作，时间复杂度为 O(n)，那有没有能将这个时间复杂度也省去的队列操作呢？这就是本小节介绍的一种特殊的队列：循环队列

顾名思义，这种队列最大的特点就在于 循环 二字，那到底要如何实现这个循环呢，让我们来看个例子：

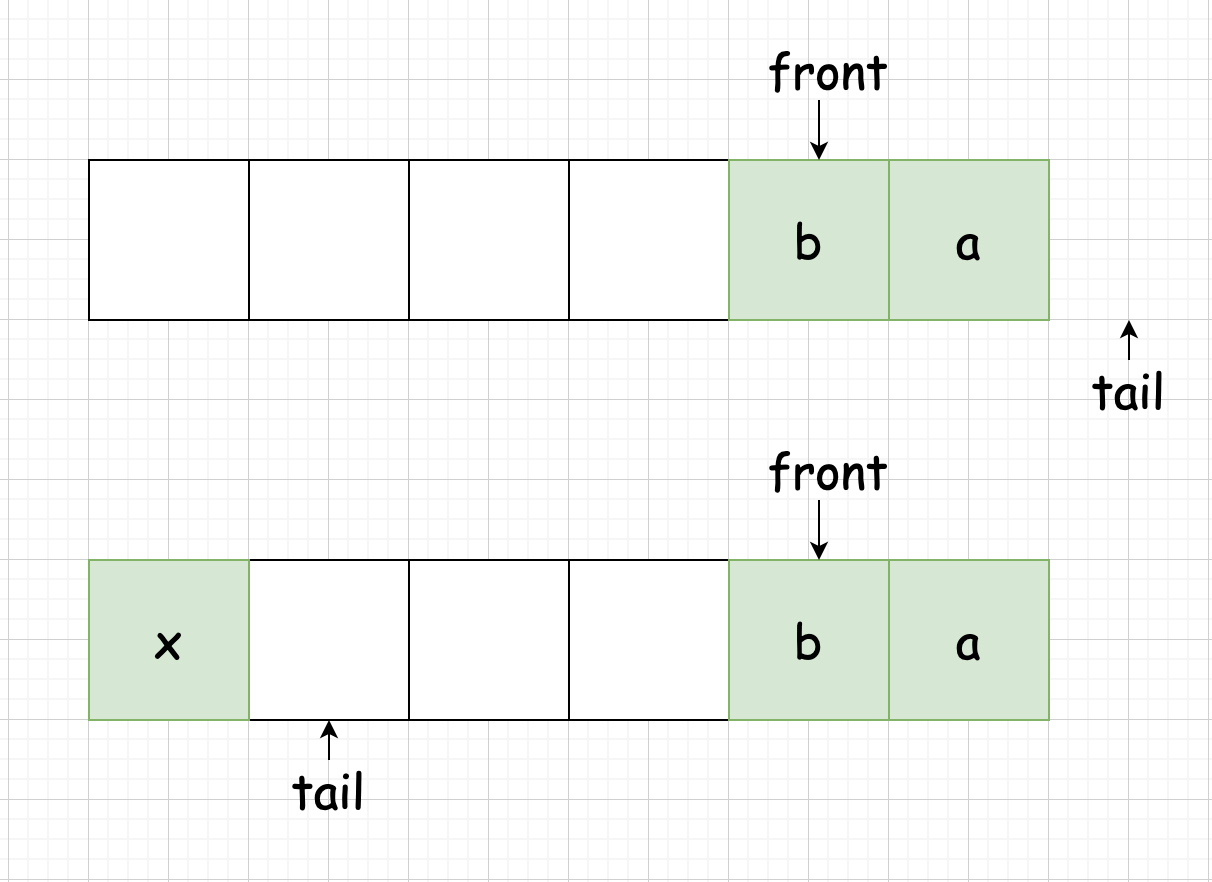
我们正常情况下，空余的空间就是左边那部分空白，如果我们能实现直接将新加入的元素直接放入左边空白的空间不就行了吗？那么用什么操作才能达到这样的效果呢，使用 取余 这个数学操作即可。

看起来的确是很 easy ，只要将 tail = (tail + 1) % capacity 即可，但是事实真的如此吗？

在前面使用数组实现队列时，我们对栈空和栈满的判断是这样的

栈空：front == tail
栈满：tail == capacity

那在循环队列中，我们应该如何实现这两个判断呢？还是举个例子，为了更加方便理解，我将数组的首尾相连，本质是还是一个数组：

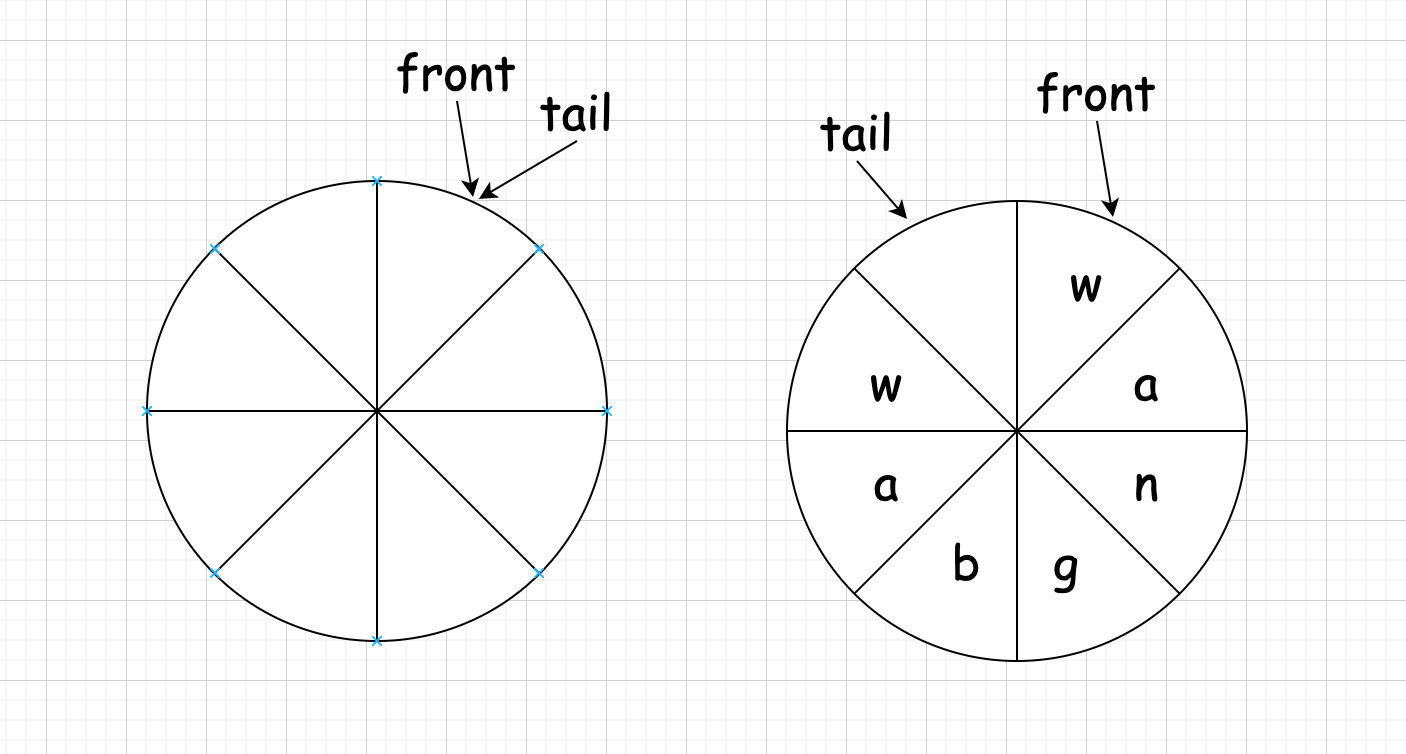
栈空：front == tail
栈满：在循环队列中用 tail == capacity 判断栈满肯定不在合适。在上面右图中，我们可以看到该循环栈还没有满，我们尝试在其中再增加一个元素，那么栈满的判断就变成了 front == tail ，这就和判断栈空一样了，所以在循环队列中，我们总是会浪费一个空间，即 tail 指向的的数据为空，也就是上面右图这样的情况，那么此时判断栈满的条件就变成了： (tail + 1) % capacity == front

上代码：

public class LC0000CycleQueue {

    private String[] elements;

    private int capacity = 0;

    private int front = 0;

    private int tail = 0;

    public LC0000CycleQueue(int n) {
        elements = new String[n];
        capacity = n;
    }

    // enqueue
    public boolean enqueue(String element) {
        // judging queue is full
        if ((tail + 1) % capacity == front) return false;
        elements[tail] = element;
        tail = (tail + 1) % capacity;
        return true;
    }

    // dequeue
    public String dequeue() {
        // judging queue is empty
        if (front == tail) return null;
        String res = elements[front];
        front = (front + 1) % capacity;
        return res;
    }
}

4.2 优先队列

这一小节介绍一下另一种特殊的队列：优先队列。老规矩，先说一下特性：

本质上还是队列，所以队列该有的操作它都有
但是它的 enqueue 和 dequeue 的操作结果可能与正常的队列结果不一样：

enqueue : 插入一个元素

dequeue : 删除最小值操作（返回并删除最小元素）或删除最大值操作（返回并删除最大元素）

优先队列的主要操作：

优先队列是元素的容器，每个元素有一个相关的键值；

insert(key, data)：插入键值为key的数据到优先队列中，元素以其key进行排序；
deleteMin/deleteMax：删除并返回最小/最大键值的元素；
getMinimum/getMaximum：返回最小/最大剑指的元素，但不删除它；

优先队列的辅助操作：

第k最小/第k最大：返回优先队列中键值为第k个最小/最大的元素；
大小（size）：返回优先队列中的元素个数；
堆排序（Heap Sort）：基于键值的优先级将优先队列中的元素进行排序；

优先队列基于什么实现最好？

实现	插入	删除	寻找最小值
无序数组	1	n	n
无序链表	1	n	n
有序数组	n	1	1
有序链表	n	1	1
二叉搜索树	logn(平均)	logn(平均)	logn(平均)
平衡二叉搜索树	logn	logn	logn
二叉堆	logn	logn	1

可以看到一般的优先队列都是基于 二叉堆 实现，具体如何实现暂时不细讲，等到写到二叉堆的时候提及一下

在 LeetCode 中关于优先队列的题目也不少，最经典的就是 0023. Merge k Sorted Lists ，具体解法可以看下 0023. Merge k Sorted Lists 中的解法三，还有比较经典的 0215、0239、0264、0295、0347、0692 等等

五、Java 中的队列

在 Java 中，队列只是一个接口，如下：

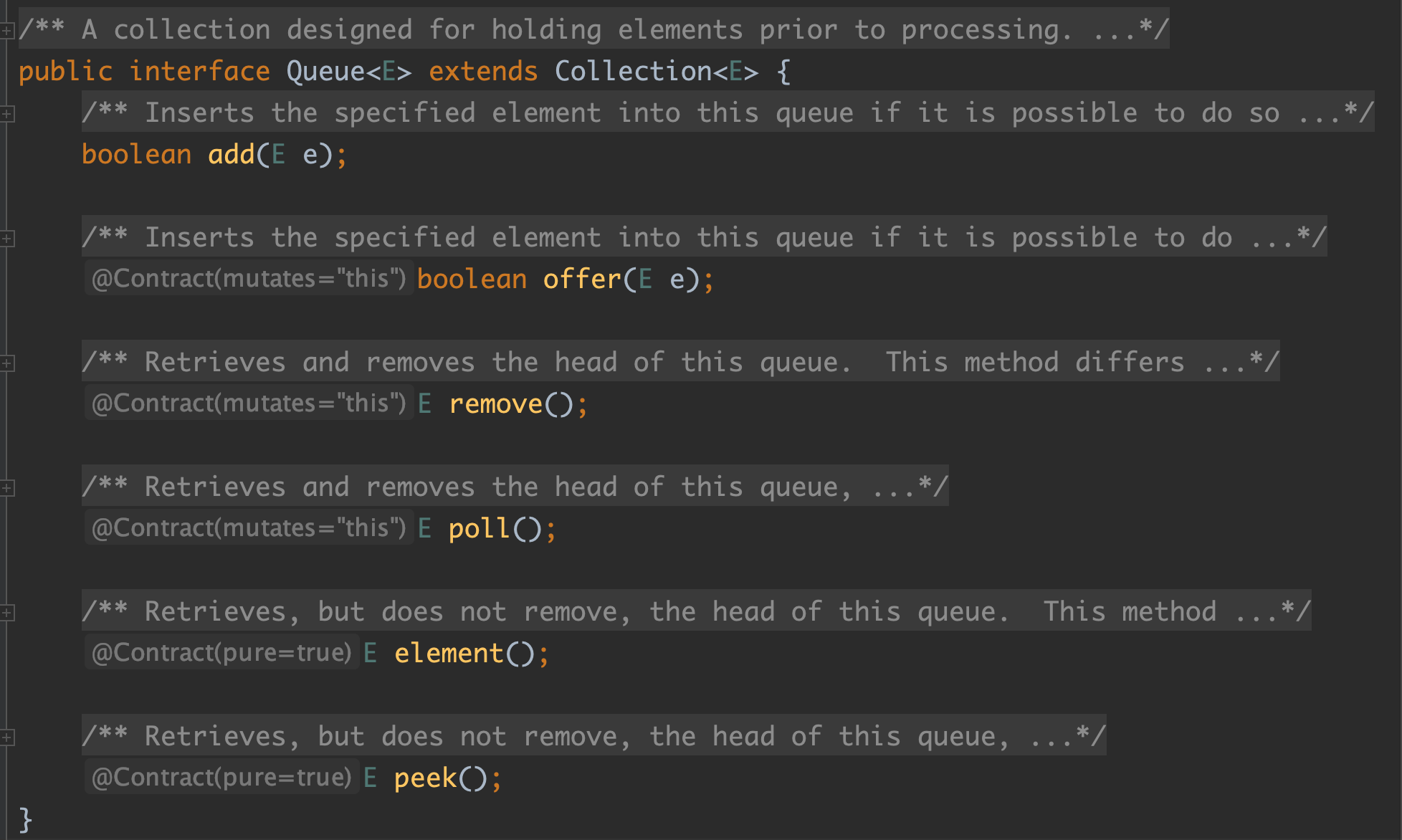
让我们来看看里面的具体实现类吧，这里优先选择上面优先队列，继承和实现类图如下：

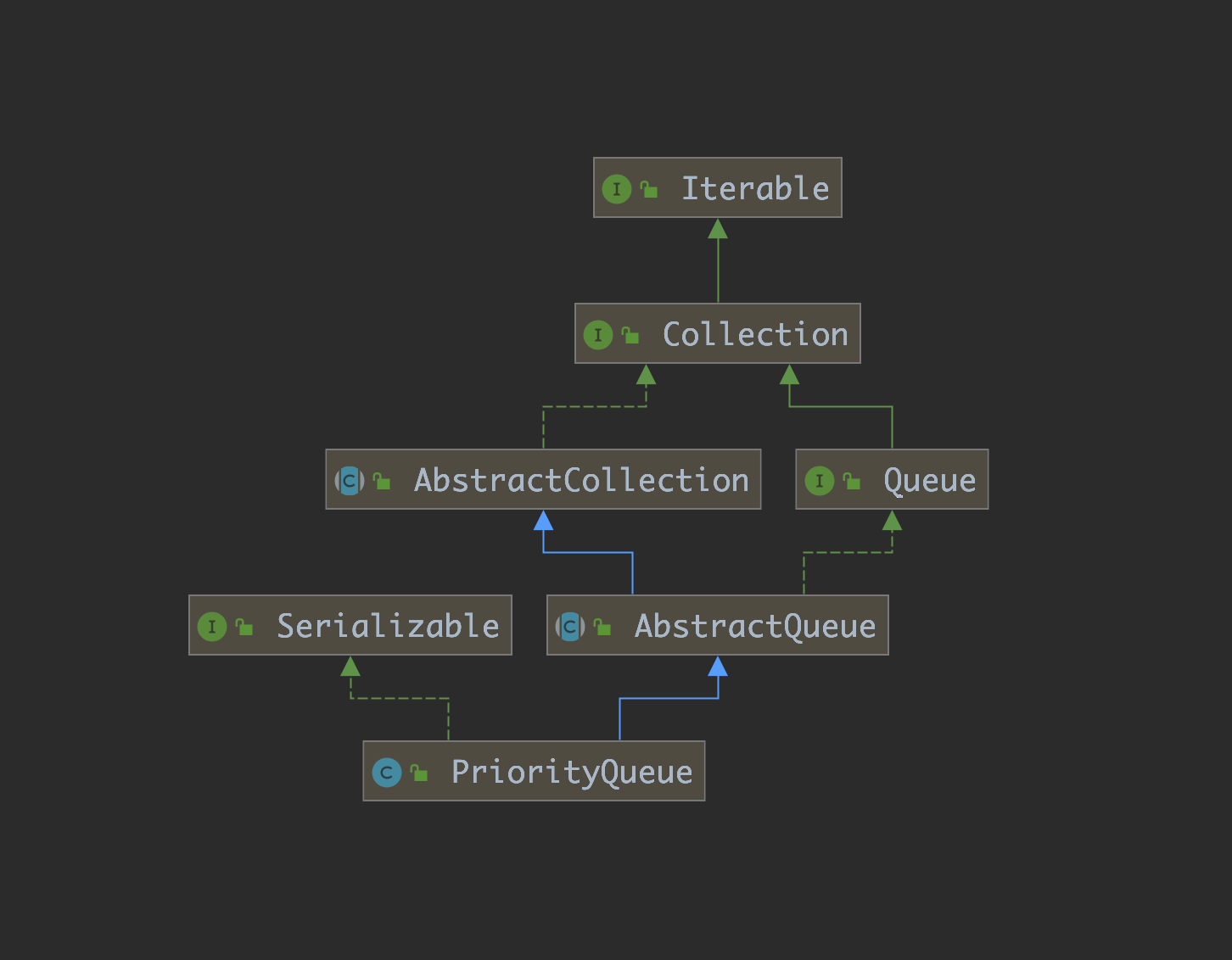
在优先队列的 Structure 中可以看到：

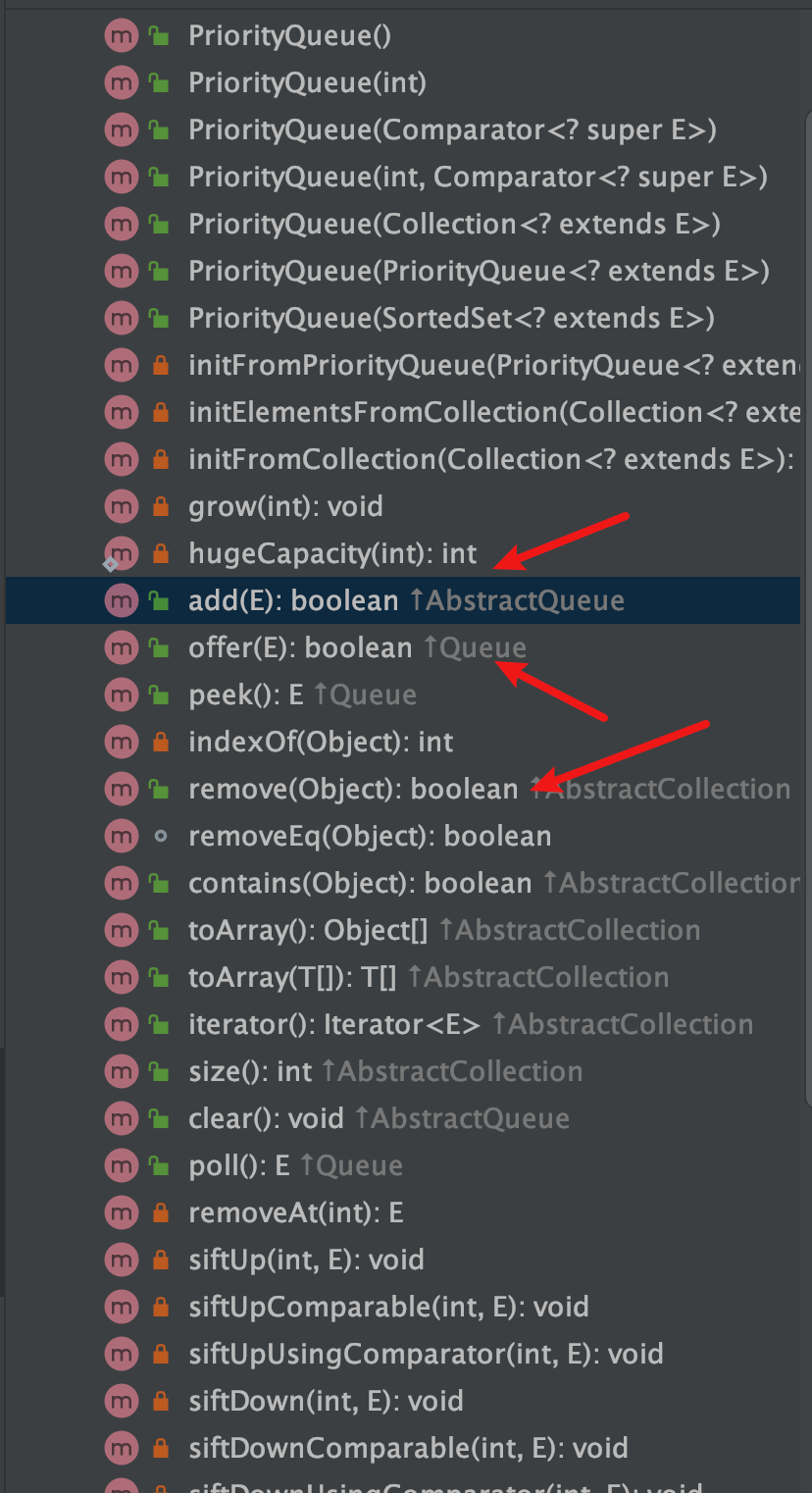
可以看到最关键的两个方法： offer 和 remove，其中 add 是调用 offer 方法的，这两个就是对应着队列中的 enqueue 和 dequeue 方法。

由于优先队列是基于二叉堆的，所以会有 上浮 和 下沉 操作，在此就不细说了

public boolean offer(E e) {
    if (e == null)
        throw new NullPointerException();
    modCount++;
    int i = size;
    if (i >= queue.length)
        grow(i + 1);
    size = i + 1;
    if (i == 0)
        queue[0] = e;
    else
        siftUp(i, e);
    return true;
}

public boolean remove(Object o) {
    int i = indexOf(o);
    if (i == -1)
        return false;
    else {
        removeAt(i);
        return true;
    }
}

private E removeAt(int i) {
    // assert i >= 0 && i < size;
    modCount++;
    int s = --size;
    if (s == i) // removed last element
        queue[i] = null;
    else {
        E moved = (E) queue[s];
        queue[s] = null;
        siftDown(i, moved);
        if (queue[i] == moved) {
            siftUp(i, moved);
            if (queue[i] != moved)
                return moved;
        }
    }
    return null;
}

更新于：2022年3月26日

Leetcode

Algorithm

Queue

Queue-Priority Quque

一、OverView 还是来填一下优先队列的坑，在前面已经介绍过队列了，而且在其中介绍了一种拥有特殊特性的队列：优先队列。在其中我们提到了，不管你是进入这个优先队列的顺序如何...

Stack--Monotonic Stack

一、OverView在前面已经提及过栈这个数据结构，在 LeetCode 中有考察过这样一种栈操作：单调栈。顾名思义，这是在栈的基础上达到单调递增或单调递减的效果。大概的过程如下：如...