WangBa's Blog

Queue-Priority Quque

重学算法系列

发布于：2020年11月25日
次浏览

一、OverView

​ 还是来填一下优先队列的坑，在前面已经介绍过 队列 了，而且在其中介绍了一种拥有特殊特性的队列：优先队列。在其中我们提到了，不管你是进入这个优先队列的顺序如何，出队的顺序是可以定制的 ( 也可以说是按照一定顺序的 )，让我们先看一个 Java 中的例子

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public class LC0000PriorityQueue {

    public static void main(String[] args) {

        Queue<Integer> queue = new PriorityQueue<>();

        // add elements
        queue.add(9);
        queue.add(1);
        queue.add(5);
        queue.add(8);
        queue.add(3);

        while (!queue.isEmpty()) {
            System.out.print(queue.poll() + " ");
        }
    }
}

结果如下：

1 3 5 8 9

只要将构造优先队列的方式改为：

1
Queue<Integer> queue = new PriorityQueue<>((x, y) -> y -x);

就可以看到结果变成了：

9 8 5 3 1

让我们来仔细研究一下，这个进队无序，出队有序的数据结构吧！

二、堆与二叉堆

为什么介绍优先队列，要先介绍 堆 这个数据机构，在上一章就已经提到过了，优先队列是基于堆完成的。

所以首先介绍一下堆：

  • 堆是一颗完全二叉树 ( 这就是前面不想介绍堆的原因，它是基于树的 )
  • 堆中所有结点的值必须大于或等于（或小于或等于）其孩子结点的值

二叉堆：每个结点最多有两个孩子结点。正常情况下，不仔细描述，一般默认堆为二叉堆。

2.1 实现堆

如果要实现一个堆，首先就要考虑使用数组实现还是链表实现，这个时候就要考虑到它的性质呢，它是一个完全二叉树，那么用数组实现它是最好的选择，来看下例子：

image-20201125165136575

可以看到，在这里面不会浪费空间，除了第 0 号索引，那是为了方便后面计算暂定，用数组还会得到下面的巨大好处：

  • 每一个结点 ( i ) 的左孩子和右孩子的索引分别为：2 * i 和 (2 * i) + 1

    example : 父结点 9 的左孩子为：1 * 2 ；右孩子为： 1 * 2 + 1

  • 每一个子结点 ( j ) 的父结点为：j / 2

    example : 子结点 1 和 子结点 3 的父结点为：4 / 2 和 5 / 2

既然我们已经确定用什么来存储了，接下来就要考虑其中的操作了，最起码的 CRUD 要有吧

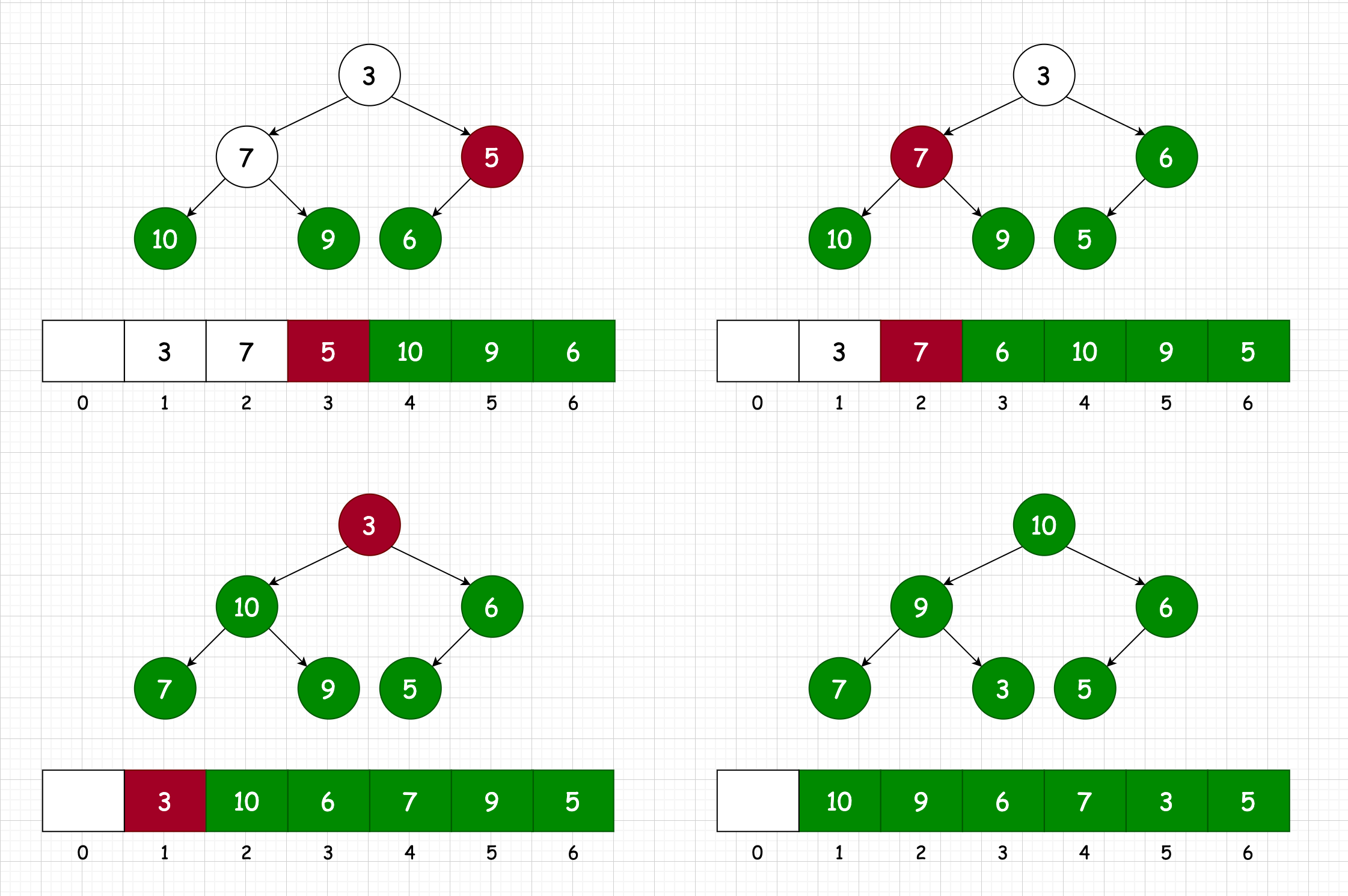
来瞅瞅增加一个元素的操作：还是用上面的那个例子吧，如果此时增加一个元素 10，那得到结果就为：

image-20201125170532356

那此时问题就出现了啊，6 明显要小于 10 啊，这就不符合堆的性质了，那么我们就要进行一个重要的操作了：

heapify (堆化)

2.2 Sift Up

像上面那个例子里面明显要把 10 放到最上方的操作，一般叫做 Sift Up (上浮)，对应的也要下沉操作，在下面进行介绍，那现在面临的问题就是怎么把 10 上浮到最上方的位置，直接与最上方位置进行交换吗？明显不行。

  • 只需要将这个结点与自己的父结点进行比较，如果符合堆的性质就不交换；如果不符合就交换父子结点

实现一下上面的例子：

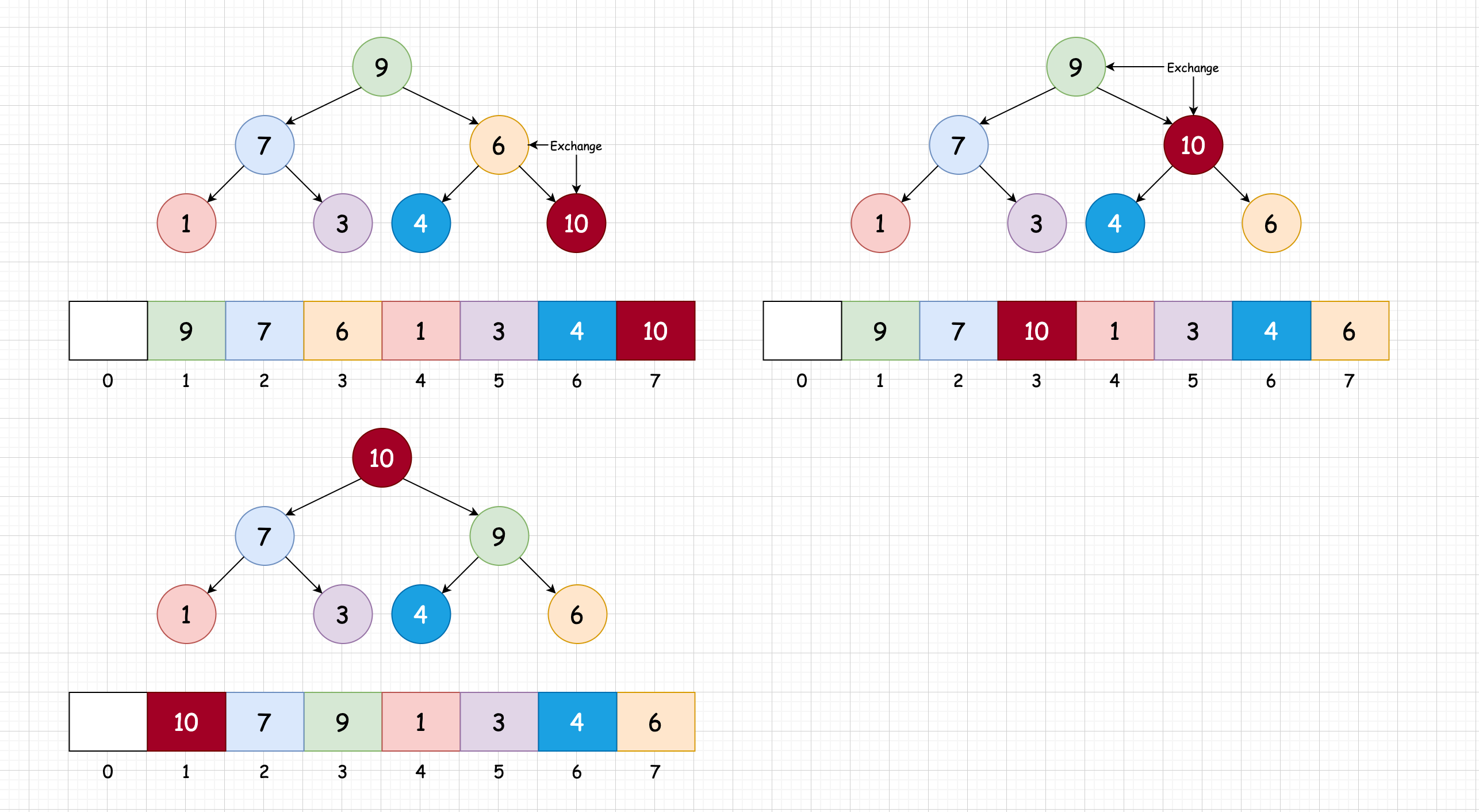
image-20201125173347010

这样就可以满足形成一个堆的条件了

2.3 Sift Down

与 Sift Up 对应的操作就是 Sift Down 操作，下浮操作一般都是处于删除之中，按照常理来说，只需要和上浮操作相反就行，理论上就是：

  • 直接将该结点删除，随后将子结点中较大的那个放到该位置，后续都进行这样的操作

但是让我们来看个例子：

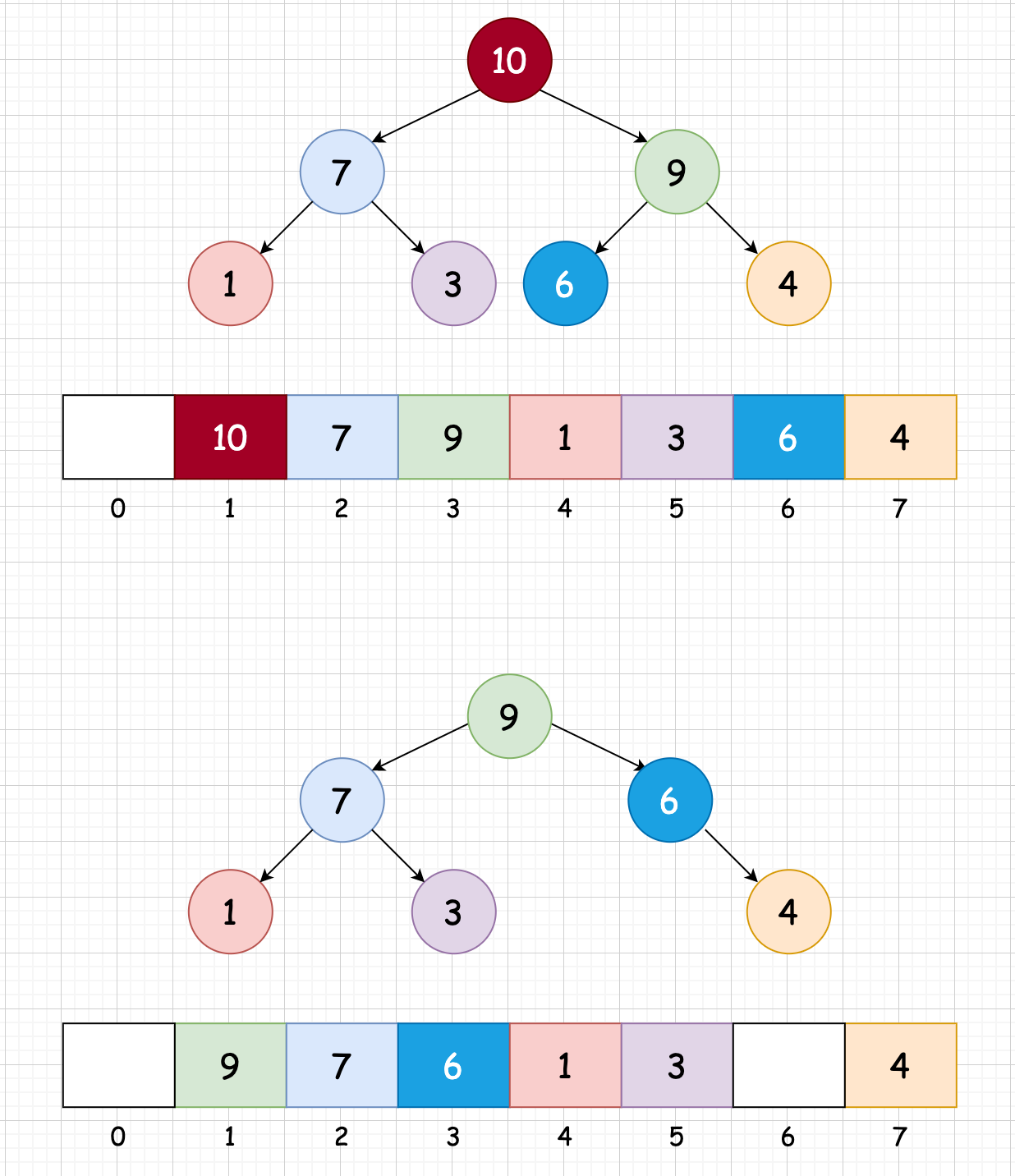
image-20201125184913889

可以看到这次进行下沉操作后，该堆并不是一个完全二叉树了，并且在数组上有多余的空间了。那么我们应该怎样去避免这种情况的发生了

我们的目的就是让它进行下沉操作后还是一个堆，只需要将要删除的结点与最后一个结点进行互换，再进行下沉操作即可

让我们来继续看上面这个例子：

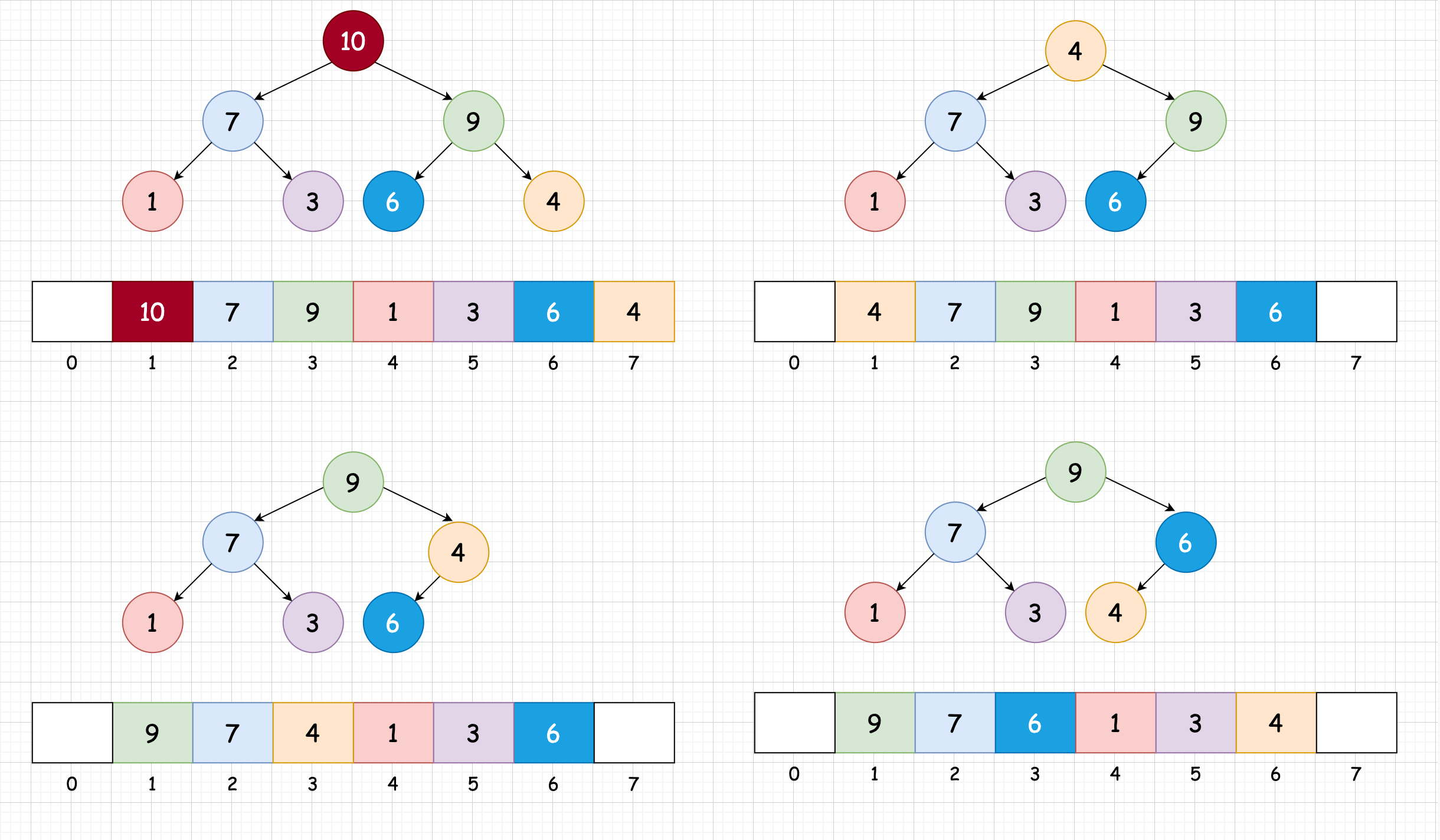
image-20201125185709215

  • 首先删除 10 ，将 最后一个元素放到该位置
  • 与子结点进行比较，进行下沉操作，将 4 与 9 互换
  • 与子结点进行比较，进行下沉操作，将 4 与 6 互换

接下来就是用代码来实现一下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
public class LC0000Heap {

    private int[] elements;

    private int capacity;

    private int count;

    public LC0000Heap(int n) {
        elements = new int[n + 1];
        capacity = n;
        count = 0;
    }

    public void add(int element) {
        if (count >= capacity) return;
        count++;
        elements[count] = element;
        siftUp(count);
    }

    private void siftUp(int i) {
        while (i > 0 && elements[i] > elements[i / 2]) {
            swap(elements, i, i / 2);
            i /= 2;
        }
    }

    private void remove() {
        if (count == 0) return;
        elements[1] = elements[count];
        count--;
        siftDown(elements, 1, count);
    }

    private void siftDown(int[] elements, int firstIndex, int lastIndex) {
        while (true) {
            int maxIndex = firstIndex;
            // compare to leftChild
            if (firstIndex * 2 <= lastIndex && elements[firstIndex] < elements[firstIndex * 2]) {
                maxIndex = firstIndex * 2;
            }
            // compare to rightChild
            if (firstIndex * 2 + 1 <= lastIndex && elements[maxIndex] < elements[firstIndex * 2 + 1]) {
                maxIndex = firstIndex * 2 + 1;
            }
            swap(elements, firstIndex, maxIndex);
            firstIndex = maxIndex;
        }
    }

    private void swap(int[] elements, int source, int target) {
        int temp = elements[source];
        elements[source] = elements[target];
        elements[target] = temp;
    }

    private int parent(int index) {
        if (index == 0) {
            throw new IllegalArgumentException("root has not parent");
        }
        return (index - 1) / 2;
    }

    private int leftChild(int index) {
        return index * 2;
    }

    private int rightChild(int index) {
        return index * 2 + 1;
    }
}

2.4 Heapify

在堆中还有一个操作就是：Heapify

该操作是对任意数组整理成堆的形式，我们可以对比一下一般对这种要求操作，和堆化操作分别是怎么实现的

  • 一般操作：将数组从 0 开始，然后逐步建立堆，时间复杂度应该为： O(nlogn)
  • 堆化操作：直接将该数组看成一个完全二叉树，随后对最后一个非叶结点到第一个结点分别进行 Sift Down 操作

如何实现堆化操作：

根据上面的描述，最关键的应该是找到第一个非叶结点，其实最后一个结点的父结点就是第一个非叶结点，下面让我们看一个实例：

image-20201125205445164

博客内容遵循 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 协议

本文永久链接是：http://wangba.me/2020/11/25/Queue-Priority-Quque/

更新于：2022年3月26日

Leetcode

Algorithm

Queue

评论